Data Mining 学习笔记
背景
我们处在信息时代,这个时代不缺乏数据,数据库中的数据量急速膨胀,但是缺乏有价值的信息(当然也缺乏获取有用信息的人)。
于是产生了KDD(knowledge discovery in dadabase),Data Mining 是KDD的一个步骤。
Data Mining 概念
从大量的,不完全的,有噪声的,模糊的,随机的数据中,提取隐含在其中的,人们事先不知道的,但又是潜在信息和知识的过程。
知识发现(KDD)是“数据挖掘”的广义说法;数据挖掘是知识发现过程的核心。
Similarity and Dissimilarity
相似度一般取值[0,1],而不相似度最小取0(eg:Distace)
Minkowski Distance(明式距离)
$$\sqrt[h]{\sum|x_i-y_i|^h}$$
又被成为L-h norm
特殊情况
1. 哈弗曼距离(L-1 norm)
2. 欧氏距离(L-2 norm)
3. supuremum距离,或者称为棋盘距离
Cosin Similarity(余弦相似度)
$$\cos(\theta)=\frac{a\cdot b}{||a||\times||b||}$$
数据预处理
Data Preprocessing 主要步骤
1. Data Cleaning(missing,noisy,inconsistent)
2. Data Integration
3. Data Reduction
4. Data Transformation
Data Cleaning:处理missing data方法:
the most probable value: inference-based (基于推理的)such as Bayesian formula or decision tree.
Data Cleaning:处理noisy data方法:
Binning (分级)
first sort data and partition into (equal-frequency) bins
then one can smooth by bin means, smooth by bin median, smooth by bin boundaries, etc.
Regression
smooth by fitting the data into regression functions
Clustering
detect and remove outliers
Combined computer and human inspection (人机检查)
detect suspicious (可疑的) values and check by human (e.g., deal with possible outliers)
Data Integration(数据整合)
含义:Combines data from multiple sources into a coherent store (统一存储)
Handling Redundancy in Data Integration
1. 不同属性表示同一个意思(Object identification)
2. 派生数据(Derivable data)
Detection of redundant attributes
1. correlation analysis
2. covariance analysis

${\sigma} _A \sigma_B$是标准差
$r_{A,B}>0$ ,正相关
$r_{A,B}=0$ : 独立
$r_{A,B}<0$ : 负相关
$$
ov(A,B)=E(A\cdot B)-\bar A\bar B
$$
Data Reduction
方法:
1. Dimensionality reduction
2. Numerosity reduction
3. Data compression
Dimensionality reduction
含义:remove unimportant attributes
方法:
1. Wavelet transforms(小波变换)
2. Principal Components Analysis (PCA)
3. Feature subset selection, feature creation
特征提取与特征选择
特征提取通过投影变换降维,它生成新特征。典型用途:图像,文档特征提取。
特征选择从给定高维数据中选出一组最具描述性的有效特征,不生成新特征。典型用途:基因选择。
Numerosity Reduction
含义:Reduce data volume by choosing alternative, smaller forms (in volume ) of data representation
方法:
1. Parametric methods
2. Non-parametric methods
Parametric Data Reduction
1. Linear regression
2. Multiple regression
3. Log-linear model
Non-parametric Data Reduction
1. histograms
2. clustering
3. sampling
Data Compression
含义:
A function that maps the entire set of values of a given attribute to a new set of replacement values s.t. each old value can be identified with one of the new values.
方法:
1. Smoothing: Remove noise from data
2. Attribute/feature construction
3. Aggregation(聚合)
4. Normalization: Scaled to fall within a smaller, specified range
关联规则
概念:项集,事物,关联规则,事物标识
项集
任意项的集合
k-项集
包含k个项的项集
频繁项集
概念:大于等于最小支持度的项集
支持度
S(A=>B): D中包含 A 和 B 的事务数与总的事务数的比值
可信度
confidence(A => B )=P(B|A)
强规则
通常定义为那些满足最小支持度和最小可信度的规则.
1. 找出所有的频繁项集(满足最小支持度)
2. 找出所有的强关联规则()由频繁项集生成关联规则,保留满足最小可信度的规则).
Apriori 算法(先验算法)
中心思想
由频繁(k-1)-项集构建候选k-项集
方法
1. 找到所有的频繁1-项集
2. 扩展频繁(k-1)-项集得到候选k-项集
3. 剪除不满足最小支持度的候选项集
Apriori 剪枝原理
若任一项集是不频繁的,则其超集不应该被生成/测试!

FP Growth算法
1. 扫描事务数据库D一次,得到频繁项的集合F及它们的支持度.将F按支持度降序排列成L,L是频繁项的列表.
2. 创建FP-树的根, 标注其为NULL.对D中的每个事务进行以下操作:根据 L中的次序对事务中的频繁项进行选择和排序. 设事务中的已排序的频繁项列表为[p|P],其中p表示第一个元素,P表示剩余的列表.调用insert_Tree([p|P],T).


Data Classification
概念:
分类是指把数据样本映射到一个事先定义的类中的学习过程.有监督学习。
决策树
概念:
1. 适用于离散值属性、连续值属性
2. 采用自顶向下的递归方式产生一个类似于流程图的树结构
3. 在根节点和各内部节点上选择合适的描述属性,并且根据该属性的不同取值向下建立分枝
决策树算法ID3

缺点:
1. ID3是采用“信息增益”来选择分裂属性的。虽然这是一种有效的方法,但其具有明显的倾向性,即它倾向于选择取值较多的属性;
2. ID3算法只能对描述属性为离散型属性的数据集构造决策树
决策树算法C4.5
概念:
C4.5既可以处理离散型描述属性,也可以处理连续型描述属性
步骤:
1. 对于连续值描述属性,C4.5将其转换为离散值属性
2. 把某个结点上的数据按照连续型描述属性的具体取值,由小到大进行排序
3. 在{A1c,A2c,…,Atotalc}中生成total-1个分割点
4. 第i个分割点的取值设置vi=(Aic+A(i+1)c)/2
5. 每个分割点将数据集划分为两个子集
6. 挑选最适合的分割点对连续属性离散化
SVM
概念:
1. 可以分*线性*以及*非线性*数据
2. 通过非线性映射(noliner mapping)把原始训练数据转换到高维
3. 在新维度里寻找超平面(hyperplane),超平面可以将两类分开
4. 通过support vectors 以及 margins 来寻找超平面
KNN
lazy learning vs eager learning
Lazy learning (e.g., instance-based learning): Simply stores training data (or only minor processing) and waits until it is given a test tuple
Eager learning: Given a set of training tuples, constructs a classification model before receiving new (e.g., test) data to classify
Lazy: less time in training but more time in predicting
Top 10 Data Mining Algorithm
1. C4.5
2. k-means
3. SVM (Support Vector Machines)
4. Apriori
5. EM (Expectation Maximization)
6. PageRank (网页排名)
7. AdaBoost
8. kNN
9. Naive Bayes
10. CART
Bayesian Networks and Classification
Two components:
(1) A directed acyclic graph 有向无环图 (called a structure)
(2) a set of conditional probability tables (CPTs)
概念
先验概率:根据历史的资料或主观判断所确定的各种时间发生的概率
后验概率:通过贝叶斯公式,结合调查等方式获取了新的附加信息,对先验概率修正后得到的更符合实际的概率
条件概率:某事件发生后该事件的发生概率
条件概率公式:$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$
全概率公式:$P(A)=\sum_{i=1}^{n}P(B_i)P(A|B_i)$
贝叶斯公式:$P(B_i|A)=\frac{P{B_i}P(A|Bi)}{\sum{i=1}^{n}P(B_i)P(A|B_i)}$
神经网络
Genetic Algorithms

粗糙集
概念:
粗糙集(Rough Set,RS)理论
波兰数学家Z.Pawlak于1982年提出
不完整性和不精确性的数学工具
分析和处理不完备性数据
发现数据间隐藏的关系
揭示潜在规律
等价关系:
设R为定义在集合A上的一个关系,若R是自反的,对称的和传递的,则称R为等价关系。
等价类
设R为集合A上的等价关系,对任何a∈A,集合[a]R={x|x∈A,aRx}称为元素a形成的R等价类。由等价类的定义可知[a]R是非空的,因为a∈[a]R
下近似集
一个知识库K=(U,R),令XU且R为U上一等价关系,X的下近似集就是对于知识R的能完全确定地归入集合X的对象的集合
上近似集
X的上近似集是知识R的在U中一定和可能归入集合X的对象的集合
正域
$$POSR(X) = R_-(X)$$
负域
$$NEGR(X) = UR^-(X)$$
边界
$$BNR(X) = R^-(X)-R_-(X)$$
由等价关系R描述的对象集X的近似精度为:
$$dR(X)=\frac{card(R-(X))}{card(R^{-}(X))}$$
$card(R_-(X))$ $card(R^-(X))$ 分别为X下近似集合、上近似集合中元素的个数。
(1)如果dR(X)=0,则X是R全部不可定义的;
(2)如果dR(X)=1,则X是R全部可定义的;
(3)如果0<dR(X)<1,则X是R部分可定义的。
PR(X)=1-dR(X)反映了定义集合X的粗糙程度,也即不被关系R所描述的程度,称为X的粗糙度。
分类近似的度量
$$dR(F)=\frac{\sum{i=1}^{n}card(R_-(Xi))}{\sum{i=1}^{n}card(R^-(X_i))}$$
$$rR(F)=\frac{\sum{i=1}^ncard(R_-(X_i))}{card(U)}$$
两种方式在本质上是等价的
分类近似的度量 – 例子
一个知识库K=(U,R),其中U={x1,x2,x3,x4,x5,x6,x7,x8},一个等价关系R形成的等价类为Y1={x1,x3,x5}, Y2={x2,x4}, Y3={x6,x7,x8}。现由分类F形成的等价类: X1={x1,x2,x4}, X2={x3,x5,x8}, X3={x6,x7}。分析由R描述分类F的近似度。
解答:
R_(X1)=Y2 ={x2,x4}
R_(X2)=[]
R_(X3)=[]
R-(X1)= Y1∪Y2= {x1,x2,x3,x4,x5}
R- (X2)= Y1∪Y3= {x1,x3,x5,x6,x7,x8}
R- (X3)= Y3={x6,x7,x8}
$$d_R(F)=\frac{2+0+0}{5+6+3}=\frac{1}{7}$$
$$r_R(F)=\frac{2+0+0}{8}=\frac{1}{4}$$
因此,分类F不能被R完全定义,即部分可定义的。
等价关系简化
对于知识库K = (U,R),如果存在等价关系r∈R,使得ind(r)=ind(R),则称r是可省略的,否则,称r是不可省略的。
(1)若任意r∈R是不可省略的,则称R是独立的
(2)独立等价关系的子集也是独立的
若Q⊂R,ind(Q)=ind(P),则称Q为P的简化,记做red(P).所有简化的交集为等价关系的核,记做core(P).
知识的相对简化


知识依赖性度量
令K = (U, R)是一个知识库,P, Q R,
(1)知识Q依赖于知识P或知识P可以推导知识Q,当且仅当ind(P)ind(Q),记作P→Q;
(2)知识P和知识Q是等价的,当且仅当P→Q且Q →P,即ind(P) = ind(Q),记作P = Q;
(3)知识P和知识Q是独立的,当且仅当 且P⇨Q和Q⇨P均不成立的时候,记作P≠Q。
$$k=r_P(Q)=\frac{card(POS_P(Q))}{card(U)}$$
令K = (U, R)是一个知识库,P,Q R,当上式成立时,我们称知识Q是k(0≤k≤1)依赖于知识P,记作P→Q。
(1)当k=1时,我们称知识Q是完全依赖于知识P;
(2)当0<k<1时,则称知识Q是部分(粗糙)依赖于知识P;
(3)当k=0时,则称知识Q完全独立于知识P。
可辨识矩阵
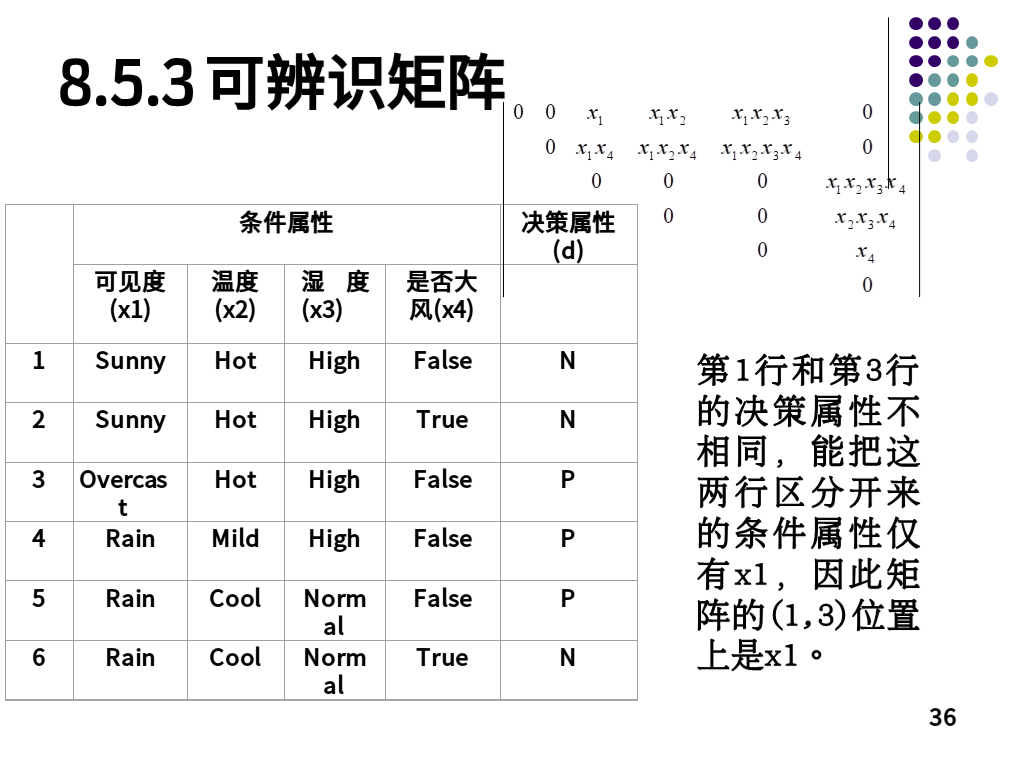
Clustering Algorithm (聚类算法)
k-means
Given k, the k-means algorithm is implemented in four steps:
1. Partition objects into k non-empty subsets
2. Compute seed points as the centroids (质心) of the clusters of the current partition (the centroid is the center, i.e., mean point, of the cluster)
3. Assign each object to the cluster with the nearest seed point
4. Go back to Step 2, stop when no more new assignment
Hierarchical Clustering(层次聚类)
概念
A hierarchical clustering method works by grouping objects into a tree of clusters.
分类
agglomerative (凝聚)
divisive (分裂)